Systolic architecture consists of an array of processing elements, where data flows between neighboring elements, synchronously, from different directions. Processing element takes data from Top, Left and output the results to Right, Bottom.
One of the key application of Systolic architecture is matrix multiplication. Here each processing element performs four operations, namely FETCH, MULTIPLICATION, SHIFT & ADDITION. As following figure depicts, "in_a", "in_b" are inputs to the processing element and "out_a", "out_b" are outputs to the processing element. "out_c" is to get the output result of each processing element.
Processing elements are arranged in the form of an array. In this case we analyze, multiplication of 3x3 matrices, which can be easily extended. Let say the two matrices are A and B. Following figure depicts how matrix A and B are fed into PE(processing element) array.
Simulation of following matrices are as follows.
Verilog modules
module top(clk,reset,a1,a2,a3,b1,b2,b3,c1,c2,c3,c4,c5,c6,c7,c8,c9);
parameter data_size=8;
input wire clk,reset;
input wire [data_size-1:0] a1,a2,a3,b1,b2,b3;
output wire [2*data_size:0] c1,c2,c3,c4,c5,c6,c7,c8,c9;
wire [data_size-1:0] a12,a23,a45,a56,a78,a89,b14,b25,b36,b47,b58,b69;
pe pe1 (.clk(clk), .reset(reset), .in_a(a1), .in_b(b1), .out_a(a12), .out_b(b14), .out_c(c1));
pe pe2 (.clk(clk), .reset(reset), .in_a(a12), .in_b(b2), .out_a(a23), .out_b(b25), .out_c(c2));
pe pe3 (.clk(clk), .reset(reset), .in_a(a23), .in_b(b3), .out_a(), .out_b(b36), .out_c(c3));
pe pe4 (.clk(clk), .reset(reset), .in_a(a2), .in_b(b14), .out_a(a45), .out_b(b47), .out_c(c4));
pe pe5 (.clk(clk), .reset(reset), .in_a(a45), .in_b(b25), .out_a(a56), .out_b(b58), .out_c(c5));
pe pe6 (.clk(clk), .reset(reset), .in_a(a56), .in_b(b36), .out_a(), .out_b(b69), .out_c(c6));
pe pe7 (.clk(clk), .reset(reset), .in_a(a3), .in_b(b47), .out_a(a78), .out_b(), .out_c(c7));
pe pe8 (.clk(clk), .reset(reset), .in_a(a78), .in_b(b58), .out_a(a89), .out_b(), .out_c(c8));
pe pe9 (.clk(clk), .reset(reset), .in_a(a89), .in_b(b69), .out_a(), .out_b(), .out_c(c9));
endmodule
module pe(clk,reset,in_a,in_b,out_a,out_b,out_c);
parameter data_size=8;
input wire reset,clk;
input wire [data_size-1:0] in_a,in_b;
output reg [2*data_size:0] out_c;
output reg [data_size-1:0] out_a,out_b;
always @(posedge clk)begin
if(reset) begin
out_a=0;
out_b=0;
out_c=0;
end
else begin
out_c=out_c+in_a*in_b;
out_a=in_a;
out_b=in_b;
end
end
endmodule
Test-bench
module test;
// Inputs
reg clk;
reg reset;
reg [7:0] a1;
reg [7:0] a2;
reg [7:0] a3;
reg [7:0] b1;
reg [7:0] b2;
reg [7:0] b3;
// Outputs
wire [16:0] c1;
wire [16:0] c2;
wire [16:0] c3;
wire [16:0] c4;
wire [16:0] c5;
wire [16:0] c6;
wire [16:0] c7;
wire [16:0] c8;
wire [16:0] c9;
// Instantiate the Unit Under Test (UUT)
top uut (
.clk(clk),
.reset(reset),
.a1(a1),
.a2(a2),
.a3(a3),
.b1(b1),
.b2(b2),
.b3(b3),
.c1(c1),
.c2(c2),
.c3(c3),
.c4(c4),
.c5(c5),
.c6(c6),
.c7(c7),
.c8(c8),
.c9(c9)
);
initial begin
// Initialize Inputs
clk = 0;
reset = 0;
a1 = 0;
a2 = 0;
a3 = 0;
b1 = 0;
b2 = 0;
b3 = 0;
// Wait 100 ns for global reset to finish
#5 reset = 1;
#5 reset = 0;
#5; a1 = 1; a2 = 0; a3 = 0; b1 = 2; b2 = 0; b3 = 0;
#10; a1 = 2; a2 = 4; a3 = 0; b1 = 4; b2 = 1; b3 = 0;
#10; a1 = 3; a2 = 5; a3 = 7; b1 = 6; b2 = 5; b3 = 3;
#10; a1 = 0; a2 = 6; a3 = 8; b1 = 0; b2 = 9; b3 = 7;
#10; a1 = 0; a2 = 0; a3 = 9; b1 = 0; b2 = 0; b3 = 8;
#10; a1 = 0; a2 = 0; a3 = 0; b1 = 0; b2 = 0; b3 = 0;
#100;
$stop;
end
initial begin
forever #5 clk = ~clk;
end
endmodule
Simulation results
Output results can be seen after 6 clock periods from the time of data insertion. (time period between a1 gets 1 and the time of yellow marker). In usual case for 3x3 matrix multiplication altogether, it takes 3x3x3 = 27 times to do the iterations and calculations. But in this case it takes lesser time (x6 times), because systolic architecture is a class of parallel pipe-lined architecture. Here is the synthesis report and timing constraints of the RTL.
Target device - xc3s500e-4fg320
Tool used - Xilinx ISE 14.3
Now lets analyze the timing differences between above hardware design and the algorithm written in C++.
C++
#include<iostream>
using namespace std;
int main()
{
int a[3][3] =
{
{1, 2, 3},
{4, 5, 6},
{7, 8, 9}
};
int b[3][3] =
{
{2, 1, 3},
{4, 5, 7},
{6, 9, 8}
};
int c[3][3];
int sum;
for(int i = 0; i < 3; i++)
{
for(int j = 0; j < 3; j++)
{
sum = 0;
for(int k = 0; k < 3; k++)
{
sum += a[i][k] * b[k][j];
}
c[i][j] = sum;
}
}
for(int i = 0; i < 3; i++)
{
for(int j = 0; j < 3; j++)
{
cout <<c[i][j]<<" ";
}
cout << endl;
}
return 0;
}
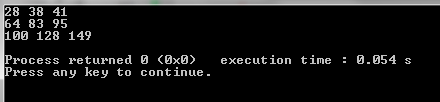
Output results
C++ execution time = 0.054s
Total delay of digital design = 7.765ns x 6 = 46.59ns





















.png)